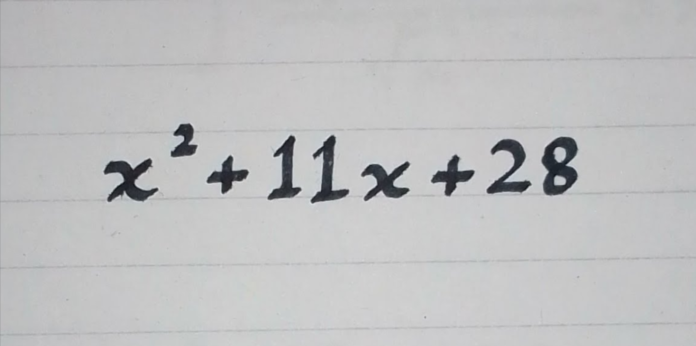Do quadratic equations confused you, but with more than one solutions for the equation, it feels complicated to determine out the easiest approach?
If sure, you have under all with the very best way to solve x² – 11x + 28 = 0. Factoring the equation, the use of the quadratic method, and finishing the rectangular are some approaches to solving the hassle. Here is the article for you to must read to understand this concept.
What is a Quadratic Equation?
To embark on this journey, we need to first draw near the essence of a quadratic equation. A quadratic equation is a second-diploma polynomial equation, characterised with the aid of the squared variable. The most essential form of a quadratic equation is expressed as: ax^2 bx c = 0
Which Are The Methods To Solve x^2-11x+28=0?
The methods to remedy the quadratic equation x²-11x+28=0 consist of factorizing expression, finishing the square, or the usage of graphical methods. This is due to the number of assumptions involved.
Therefore, it’s higher to use a complete-proof quadratic equation technique in place of successful-and-trial, time-ingesting manner to rule out the solution.
General Form of a Quadratic Equation
Understanding the overall form of x² – 11x + 28 = 0 is pivotal because it underpins the muse of those equations. By knowing this form, we’re able to results easily turn out to be aware of the coefficients ‘a,’ ‘b,’ and ‘c.’ For our particular equation, ‘a’ is 1, ‘b’ is -11, and ‘c’ is 28.
Roots of Quadratic Equations
The roots of a quadratic equation are the values of ( x ) that fulfill the equation. They constitute the factors where the parabola intersects the x-axis. There are several techniques to discover these roots, including:
- Factorization: Expressing the quadratic equation as a product of two binomials.
- Quadratic Formula: A frequent approach that uses the coefficients ( a ), ( b ), and ( c ) to locate the roots.
- Completing the Square: Transforming the equation into a great rectangular trinomial.
Graphical Representation of Quadratic Equations
In the area of x² – 11x + 28 = 0, the graphical depiction frequently takes the form of a parabola. This shaped curve gives critical insights into the behavior of those equations, with the vertex being a central point, signifying both the minimum or most of the parabola.
Applications of Quadratic equations
Quadratic equations are not just theoretical constructs; they have got practical applications in diverse fields
- Physics: Describing projectile movement, loose fall, and other phenomena.
- Engineering: Designing structures, reading forces, and optimization issues.
- Economics: Modeling fee functions, revenue features, and marketplace equilibrium analysis.
In conclusion, knowledge quadratic equations is not just about solving for ( x ); it’s about comprehending a fundamental concept that bridges various disciplines. The equation ( x2-11x+28=0 ) is a classic instance that encapsulates a majority of these elements, serving as a great specimen for exploration.
Conclusion
This post on x² – 11x + 28 = 0 has now not most effective simplified the way of solving such an equation through diverse strategies like factorization, the quadratic system, and finishing the square but has Also use in diverse fields.